Módulo de Software Libre en Educación
Exploración de la herramienta Geogebra
Verificación del teorema de Pitágoras
Inicialmente se selecciona herramienta Geogebra, para el trabajo con esta herramienta se ingresa a la página http://www.geogebra.org/cms/es/ y se observan las opciones de descarga. Geogebra es un software libre especializado para la enseñanza y aprendizaje de las matemáticas y ciencias. Al entrar a la página de descargas existe la opción de descargar el software libre y también de descargar material libre. En la descarga del software hay disponibilidad en diferentes plataformas, tanto Android, Windows, Linux, Java y Mac. Se eligió la opción de la plataforma en Windows y se inició la descarga. Con esta herramienta se pretende verificar gráficamente el teorema de Pitágoras, para esta construcción se inicia una exploración del programa. Inicialmente se encuentran dos barras en la parte superior de la ventana, la primera es una barra de menu con las opciones de archivo, edición, vista, opciones, herramientas, ventana y ayuda. Enseguida se observa una barra de herramientas con doce íconos que permiten realizar la construcción deseada. Por defecto Geogebra muestra en el área de trabajo los ejes de un plano cartesiano, al cual se le puede agregar cuadrículas para una mejor ubicación cartesiana de los puntos que se quieran trabajar. A través de dos íconos debajo de la barra de herramientas se puede quitar o mostrar la cuadrícula y los ejes del plano cartesiano. Para evitar confusiones se quitan los ejes del plano cartesiano y la cuadrícula, dejando el espacio en blanco para iniciar la construcción que se siguen los pasos:
1. Se selecciona el ícono de puntos y de dibujan dos puntos en cualquier lugar del plano. 2. Se selecciona el ícono de rectas y se hace click en los dos puntos anteriores para construir la recta que pasa por esos dos puntos. 3. Se selecciona el ícono de rectas perpendiculares, se hace click en la recta que ya se ha construido y aparece una recta perpendiculara a la recta inicial; esta segunda recta se arrastra hacia unos de los puntos iniciales y se ubica sobre éste. 4. Sobre la segunda recta se ubica un tercer punto. 5. Se selecciona el ícono de polígono y haciendo clik en los tres puntos dados se construye un triángulo rectángulo. 6. Para verificar que el triángulo sí es rectángulo se selecciona el ícono de ángulos y se nombra el ángulo recto, de esta manera aparecerá el rótulo mostrando que el ángulo es de 90 grados. 7. Como ya se tiene construido el triángulo, se seleccionan las rectas perpendiculares y en el menú "Edita" se selecciona "Objetos Invisibles". Esto se hace para no tener en el plano elementos distractores. 8. En las opciones que se despliegan del ícono de polígono, se selecciona polígono regular, se hace click sobre dos de los puntos del triángulo y aparece una ventana que permite escoger la cantidad de lados del polígono que se quiere construir, en esta ventana se escribe el número 4. De esta manera se contruye un cuadrado que tiene como base uno de los lados del triángulo. Este proceso se repite para los otros dos lados del triángulo rectángulo. 9. Una vez construido ese gráfico, se rotulan los valores correspondientes a las áreas de cada polígono. Para ello, en el ícono vista, se selecciona la opción de vista lagebráica allí se presenta en la parte izquierda de la pantalla una sección en la que aparecen cada uno de los objetos geométricos que se han utilizado y sus medidas. 10. Para los efectos prácticos de este recurso se mostrarán ünicamente las longitudes de los segmentos que forman el triángulo y las áreas de los cuadrados. 11. Para no mostrar los demás elementos (que se consideran no necesarios en la verificación del teorema), se seleccionan, se da click en el botón secundario del mouse y se selecciona "propiedades", alli aparece una ventana en la que se debe marcar la opción "Objeto auxiliar". Esto no permitirá ver los elementos ni en la vista algebraica, ni en la vista gráfica.
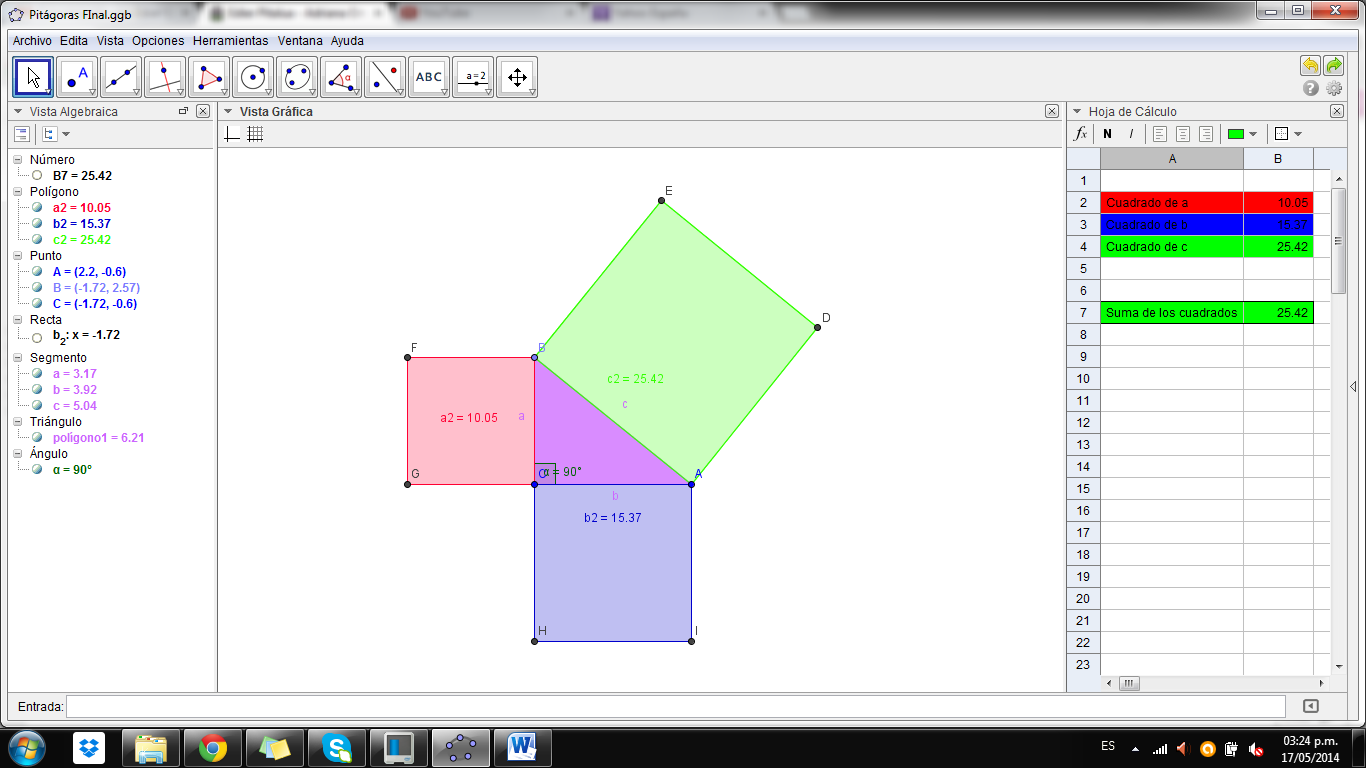
Finalmente el recurso creado queda para el uso de estudiantes de grado noveno en adelante, para la verificación del Teorema de Pitágoras, con la guía del docente. Se debe explicar al estudiante la convención de parámetros utilizados en el recurso. En la parte izquierda, en la sección de “Vista Algebraica” se puede visualizar el valor de las áreas de los cuadrados formados por los lados del triángulo (en el ítem polígono) y el valor de los lados del triángulo. En la parte central de la pantalla del programa se encuentra la sección de “Vista Gráfica” donde se puede observar el triángulo rectángulo y a partir de los lados de él se encuentran formados los cuadrados. Se pueden mover los puntos A, B y C, de forma que se pueda modificar el triángulo, pero al modificarlo siempre se va a mantener un triángulo rectángulo. Al modificar el triángulo automáticamente se ajustan los cuadrados formados a partir de sus lados. En la parte derecha del recurso se encuentra la sección “Hoja de Cáculo” donde aparecen nuevamente los valores de los cuadrados de a y b, y además la suma de dichos valores. Debajo de la suma se muestra el valor del cuadrado de c, para que así se pueda comparar el valor del cuadrado de c con la suma de los cuadrados de a y de b, verificando de esta forma el Teorema de Pitágoras. El recurso permite que se pueda modificar el triángulo, siempre manteniendo el ángulo de 90 grados. De esta manera, se puede verificar el Teorema de Pitágoras para cualquier triángulo que el estudiante quiera formar en la sección de “Vista Gráfica”, al verificar en la sección de “Hoja de Cálculo” que la suma de los cuadrados de a y b siempre corresponderá al cuadrado de c.